Designing Your Gamification Ranks to “Flow”
Preface
This whitepaper is an updated current rendition of a series of blog posts I authored when I was working at Lithium Technologies (now Khoros) as their Chief Scientist. These blog posts were previously published on the Lithsophere – an open community for sharing best practices, empirical data, and research results on everything related to online communities. When I left Lithium, this community houses a total of 882 posts I shared during the 10 years of my career there (from 2007–2018). And everything is open, freely accessible, and indexed by search engines (so findable on the internet).
However, as we all know, the only constancy in life is change. Lithium was acquired by Vista Equity Partners. Shortly after my departure, Lithium was rebranded Khoros, and the Lithosphere community is also renamed to Atlas. Although you can still find me on Atlas, all my writings are now behind the registration gate and are no longer publicly accessible.

Although I have left most of my research on social media, influence, and gamification, so I can focus on AI and ML, I still contribute to the gamification community occasionally as I am still fascinated by human behaviors. Below are a couple of recent events where I was invited as an honorary speaker to share my thoughts on gamification,
- International Conference on Software Engineering 2022
where I presented a keynote on “Fulfilling the Promise and Potential of Gamification“ - Global Gamification Hackathon 2023
where I presented a keynote on “The Gamification AI Learning Loop“
These events allowed me to reconnect with friends and get reacquainted with gamification practitioners from around the world. And quite a few have asked me about a series of gamification posts I wrote on rank design and the linear-increment ranking formula I’ve developed. So by popular demand, I am rewriting and recompiling all those posts into this whitepaper. And it is republished here so it will remain freely accessible to everyone who is interested in this collection of research.
1. Introduction: Flow – An Optimal Mental State
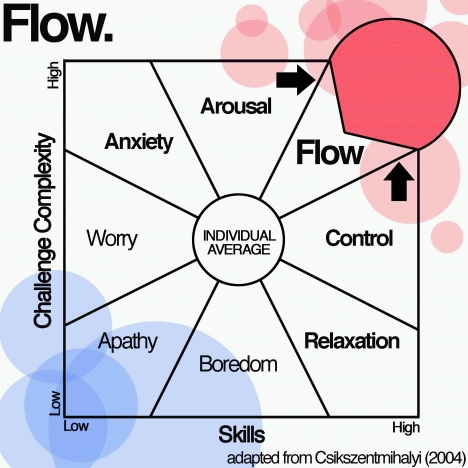
Have you ever experienced a time when you were so immersed in what you were doing that you forgot about your physical feelings and the passage of time? This highly rewarding mental state is known as flow, and it is studied and characterized by a renowned psychologist Mihaly Csikszentmihalyi.
I had the great pleasure of hearing Prof. Csikszentmihalyi himself speak on this topic at the Persuasive2009 conference. The talk was enlightening and made me understand why I sometimes forgot to eat or sleep when deeply absorbed in solving a problem.
According to Csikszentmihalyi, flow is an optimal state that can be attained when the challenges we encounter are matched to our ability. When the task is slightly too easy (or too hard) we fall out of flow and go into a state where we feel in control (or aroused if the task is slightly too hard). When the task difficulty greatly exceeds our skills, we are likely to experience anxiety. And if the task challenges do not come close to our ability, we will often experience boredom (see Figure 1.1).
Picking a task that is just challenging enough for us to move into the flow state is not easy because the tasks we encounter do not have a continuous range of difficulty. Moreover, the exact level of challenge for a task is difficult to gauge. In an attempt to challenge ourselves, we often pick a task that is too hard and go into a state of anxiety. This is why many people like staying in their comfort zone of control and relaxation and do not like challenging themselves. Consequently, flow is not a common mental state.
As illustrated in Figure 1.1, this also implies that when we are in a state of control or relaxation, we simply have to challenge ourselves and pick a more difficult task to get back into flow. However, if we picked a task that is too hard, we must learn and increase our skills gradually in order to move back into flow. Therefore, we learn the most when we are in the arousal state.
Although flow is not common, Prof. Csikszentmihalyi has mentioned that they are more prevalent in creative professionals, such as artists, composers, poets, scientists, mathematicians, etc… This is because these professions require much self-challenge to create something novel and original. Due to the distinctive gaming heritage of Lithium (now Khoros), we know another group of people who often experience flow. Can you guess? Yes, they are gamers. If you know friends who are into gaming, or if you have teenage children who are addicted to computer games, you will know what I am talking about. They will play tirelessly for hours, if not days, straight.
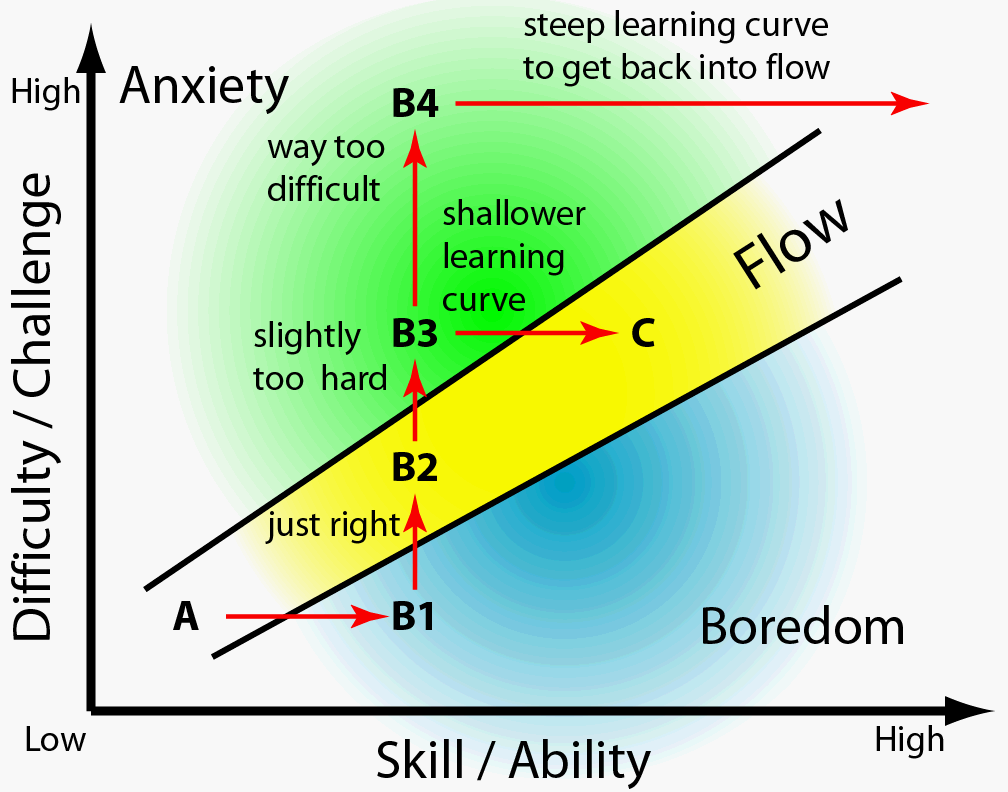
So what is it about video games that enable people to move into flow so easily? Actually, games in general (not limited to video games) can create an artificial environment where the task difficulty is well-controlled and increase gradually. This makes it much easier for gamers to pick a just-challenging-enough game to move them into flow (B2 in Figure 1.2). Even if a gamer accidentally chose something too difficult, it would most likely not be something totally beyond his skill. So, they would experience arousal (B3 in Figure 1.2) rather than anxiety or worry (B4 in Figure 1.2), which is undesirable. In the arousal state, gamers only have to learn a little bit to increase their skills sufficiently to move back into flow. This will in turn encourage gamers to take on more challenges. This feedback dynamic is what makes so many gamers addicted to playing their favorite games.
As a practitioner of this theory, Lithium knew all along that the reason the superusers within their community would spend 8 hours online answering questions is precisely the same reason that a gamer would play for days without sleeping. In fact, the Lithium platform is built upon their deep understanding of various gaming and social dynamics. The control -> arousal -> flow dynamic is just one of many that are deeply ingrained in their rich and flexible reputation engine. This is the reason they are able to attract and keep those superusers who will spend many hours in their communities. Moreover, because flow is inherently a rewarding and desirable mental state, superusers are often happy to volunteer their time and effort. To them, it’s just like playing a game.
2. Spacing the Rungs of Your Rank Ladder
A well-designed game usually has many levels. with the difficulty between levels increasing slowly so that gamers can easily find challenges that match their skills. By extrapolation, an engaging rank ladder for the users should mimic the gradually increasing difficulty levels of a game. Although the ranking criteria may depend on any combination of metrics we collect, I will use the most common criterion, post count, as an illustrative example.
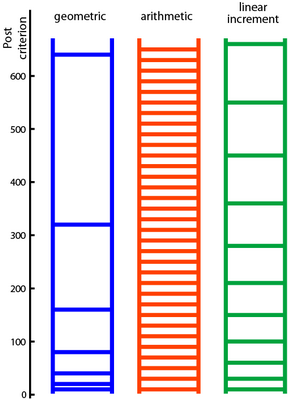
A common mistake that many communities make is to use the convenient geometric progression as the post criterion for promotion to successively higher ranks. A geometric progression is a numerical sequence where successive terms are obtained by multiplying the current term by a fixed and common ratio.
For example, the post requirement for the first rank might be \(10\) posts, and then successive ranks require \(20, 40, 80, 160, 320, 640, 1280\), etc (blue ladder in Figure 2.1). Geometric progressions are terrible as ranking criteria because they grow very rapidly. In fact, the growth rate of geometric progressions is exponential! The example sequence above, with a common ratio of 2, grew over 1000 in just 8 terms.
So how should you space the rungs of your rank ladder? There are two possible solutions. First is an arithmetic progression, where the successive terms are obtained by adding a fixed value to the current term.
For example, the first rank might require \(10\) posts, and then the higher ranks require \(30, 50, 70, 90, 110, 130, 150, 170, 190\), etc (red ladder in Figure 2.1). Because arithmetic progressions grow more slowly than geometric progressions, they are better suited for ranking criteria. However, because such ranking criteria are very regular, they may be too predictable to challenge highly competitive superusers.
If you want to challenge your superusers, I recommend using a sequence with a linear increment scheme, where the difference between successive terms grows linearly. For example, the first rank might require \(10\) post, then subsequently, \(30, 60, 100, 150, 210, 280, 360, 450, 550\) etc (green ladder in Figure 2.1). Unlike the arithmetic progression, where the difference between successive terms is always 20, the difference between successive terms of this sequence increases linearly: \(30-10=20, 60-30=30, 100-60=40\), etc. This sequence can be generated by the rank criterion formula,
\[c(n)=\frac{d}{2} (n+n^2)\]
Here \(d\) is the incremental difference between successive terms, and \(n\) is the rank number. The example I presented above has an incremental difference of \(d=10\), so it can be generated by
\[c(n)=\frac{10}{2} (n+n^2)=5×(n+n^2)\]
You can easily check that the third term \((n=3)\) is \(5×(3+3^2)=5×12=60\), and the forth term \((n=4)\) is \(5×(4+4^2)=5×20=100\), and so on.
Keep in mind, the key is to have small gaps between the early rungs of your rank ladder. An ideal ladder might start with a geometric progression, since the early terms of a geometric progression are fairly closely spaced. As the gaps between the ranks increase, you can control them by switching the ranking criteria to a linear incremental scheme. And finally, you can move to an arithmetic progression to prevent the gap size between ranks from growing so large that it is nearly impossible to move up the ladder.
3. Know Your Top Gamers (a.k.a. Superusers)!
An important mechanism for getting into the state of flow is to have a balance between ability and challenge. In an online community, this means having a set of ranking criteria that matches your superusers’ ability. If the criteria are too easy, superusers will quickly reach the top rank and become bored. But if the criteria are too difficult, superusers will become frustrated over their lack of advancement. In either case, the risk is that superusers will give up trying and abandon the community eventually.
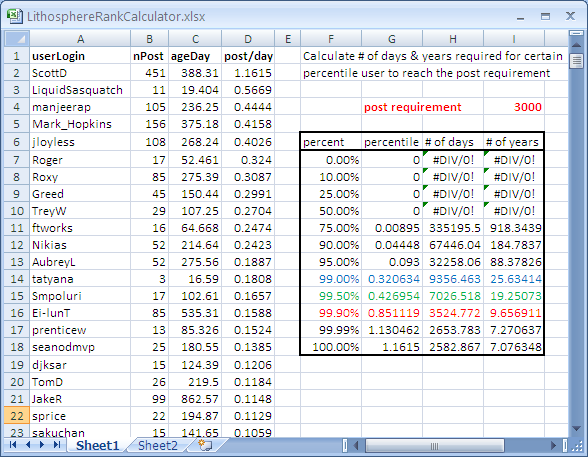
Knowing your superusers is the key to designing a rank structure that matches their capability. Using the Lithosphere community as an example, this can be done simply by computing the post rate for all users that have registered for more than 2 weeks on the community. Upon collecting the data from Lithosphere, I will illustrate this calculation below (see Excel screenshot below in Figure 3.1). As of June 6, 2009, Lithosphere had 524 members who have registration age of more than 14 days (2 weeks). Column B shows the total post count by these users (including blogs, ideas, comments, and replies, but excluding deleted messages). Then I divided each user’s post count by their respective registration age in days (column C) and sorted the resulting post rate (column D).
Now, if you believe the 90-9-1 rule, the top 1% (i.e. the 99 percentile) should be precisely your superusers. In our experience, the fraction of superusers consists of only about 0.1% of the community population. Sean O’Driscoll (an online community expert) also claimed that only 0.5% of the members in his data are superusers. If we use our conservative estimate of 0.1%, the capability of Lithosphere’s superusers is simply the 99.9 percentile of the post rates. Capability, in this example, means how fast your superusers can post.
Using Excel’s percentile function, you can calculate the 99, 99.5, or 99.9 percentile values from the post rates (column D). From the Excel screenshot, we can see that the 99.9 percentile post rate is about 0.851 posts/day. This is the approximate capability of the superusers on Lithosphere. The superusers in your community will have a different number, and communities with very active superusers will have a larger number. I’ve certainly seen communities with superusers posting up to 35 posts/day. Armed with this knowledge of your superusers, you can now scale your community’s rank ladder so that its ranking criteria match your superusers’ capability.
Our empirical data suggests that, on average, community members expect a promotion to higher rank once every month. This would require an average of 12 ranks in 1 year, or 24 ranks in 2 years. Using the ranking criteria formula I presented in Section 2, we can calculate the post requirement for the 24th rank. If we use the incremental difference of 10 as in Section 2, then \(c(24)=(10/2)×(24+24^2)=5×(24+576)=3000\) posts. For Lithosphere superusers (posting 0.851 posts/day), this would take them roughly 3525 days or 9.7 years to reach a post count of 3000, because (3000 posts)÷(0.851 posts/day)=3525 days.
Clearly this ranking criterion is too challenging for the Lithosphere superusers. At 0.851 posts/day, we can only expect the Lithosphere superusers to post about 621 posts in 2 years, since (2 years)×(365 days/year)×(0.851 posts/day)=621 posts. Even if we make a wild speculation that the superusers capability will double in 2 year, this would only brings the expected post count to \(621×200\%=1242\) posts, nowhere near 3000 posts.
Clearly, we need to rescale this rank structure. With simple algebra, I solved for the incremental difference as a function of the post criterion from the formula I presented in Section 2:
\[d=\frac{2\cdot c(n)}{n+n^2}\]
But what do we plug in for the post criterion \(c(n)\)?
Since Lithosphere is a young community, the superusers definitely have room for improvement. I will assume a 20% yearly increase in the superusers’ capability, so that their expected post count over 2 years could potentially reach (621 post)×(120%)×(120%)=894 posts. Therefore roughly 894 posts should be the proper post requirement for the 24th rank, hence \(d=(2×894)÷(24+24^2)=1789/600=2.98\).
Rounding this to 3, we may now generate the optimal ranking criteria that are match to the capability of the superusers on Lithosphere. The post requirement for the first rank is \(3\) posts, then \(9, 18, 30, 45, 63, 84, 108, 135, 165, 198, 234, 273, 315, 360, 408, 459, 513, 570, 630, 693, 759, 828\), and finally \(900\) posts at the 24th rank. Even if Lithosphere’s superusers did not improve their capability at all, they would have gotten approximately \(621\) posts in 2 years and ascend through 19 ranks requiring \(570\) posts.
So, is your rank ladder too easy or too difficult for your superusers? A sanity check by computing the post rate of just the top users in your community and comparing that to the post requirement of the top rank can quickly tell you if your rank structure makes sense. A rank structure that is designed to “flow” could engage and captivate your superusers with superior efficacy.
If you are interested, here is a video recording of a workshop I hosted at Gamification Europe 2017. Within this short workshop, there is a section where I covered the theory behind the linear increment ranking criteria. And since it’s a hands-on workshop, I also worked through an example to demonstrate how to use it.
4. Flow with Your Most Prolific Superusers
In a benchmark study I conducted, we found that healthy and vibrant communities that have many superusers generally have a large number of ranks. In fact, the benchmark list of top communities has an average of 31 non-role-based ranks (ranks that are achievable through participation). If we include role-based ranks (that were assigned), the average is 59. Among these top communities, the number of ranks goes as high as 134 ranks. But does this apply to your community? The important questions are: How many ranks does YOUR community need, and how many is enough?
The answer is that you need as many ranks as necessary to keep your most active superuser engaged. The exact number will depend on how prolific your most active superuser is. I will illustrate this with the calculation on Lithosphere again. In Section 3, we’ve designed an optimal rank ladder for Lithosphere. The post requirement for each rank are: 3 posts, 9, 18, 30, 45, 63, 84, 108, 135, 165, 198, 234, 273, 315, 360, 408, 459, 513, 570, 630, 693, 759, 828, and finally 900 posts at the 24th rank.
We’ve also calculated the post rate for all users who have been in the community for more than 2 weeks and sorted them. You will see that ScottD is the most active superuser on Lithosphere (he also happens to be the community admin, but let’s ignore that for now). He has posted 451 messages in total and his post rate is 1.16 posts/day. If ScottD wasn’t our admin, he would be on the 16th rank now. So the proposed rank ladder with 24 levels is definitely enough for now.
A natural question is when will this rank ladder become insufficient? If ScottD posts 450 more messages, his post count will exceed 900 (the highest rank). After that, his contribution will no longer be rewarded by this rank ladder. Soon after, he may become bored with the community. How long would that take? Since we have ScottD’s post rate, 450 more posts would take him about (450 post)÷(1.16 posts/day)=388 days. So in a little more than a year, it will be time to adjust this rank ladder.
What do we need to do a year from now to keep ScottD engaged in his personal flow state? Add more ranks! But how should we set the rank criteria? Remember, if it’s too easy, ScottD will be bored, and if too hard, he might become frustrated and leave.
Note that the gap between the 23rd and 24th rung of the rank ladder is (900–828)=72 posts. For typical Lithosphere superusers with post rate of 0.851 posts/day, this will take them about (72 posts)÷(0.851 posts/day)=85 days, which is almost 3 months. Even for ScottD, the most prolific superusers on Lithosphere, it will take him about (72 posts)÷(1.16 posts/day)=62 days, which is about 2 months. This means the gaps between the top rungs of our existing rank ladder is already challenging for our superuser.
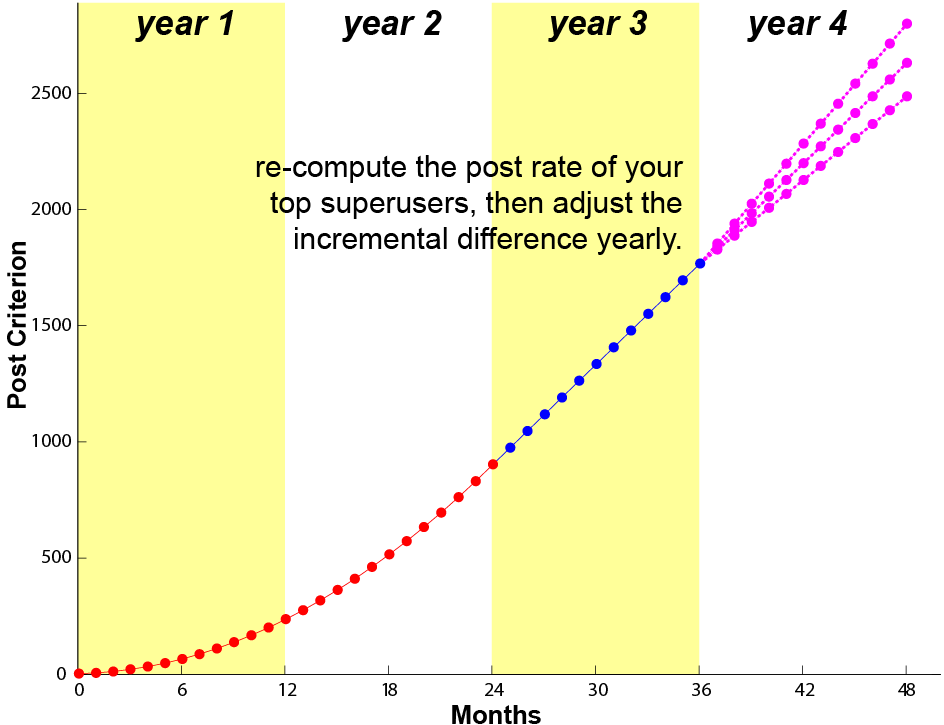
So after the 24 linearly incremental ranks that are designed to engage the superusers of Lithosphere for 2 years, it is a good time to switch to the arithmetic progression (a.k.a linear progression), which has a constant growth rate. The logical choice is to continue the rung spacing between the top ranks of the existing rank ladder. How many ranks we add depends on how soon we want to adjust the rank ladder again. If we want to challenge ScottD with the appropriate difficulty for 1 more year, we will need to add at least 6 ranks, starting with the 25th rank requiring 972 posts, and then spaced evenly every 72 posts thereafter.
Why wouldn’t we just add 60 more ranks and be good for the next 10 years? You can, but I certainly would not recommend that because ScottD’s capability may change. Perhaps another more prolific superuser will come along, or some other superusers may surpass ScottD. So we may need to change the spacing of the linear progression again the following year. In general, it is a good idea to re-compute the post rate of your top superusers yearly and adapt the post criteria to keep the “flow” with your superusers.
5. Give Your Superusers a Little Surprise
Part of the fun and the challenge in gaming is the unpredictable elements of the games. The player can never truly know the outcome of his play. When the gamer has figured out the game, he moves into the control state. When he is able to predict the outcome, the game is probably too easy for him. And soon he will find the game boring and move on to something more challenging. Likewise, a fun and challenging rank ladder should be cryptic, and it is best when there are some elements of surprise built in. In Section 4, I talked about switching after year 2 to a more regular and predictable arithmetic progression (a.k.a. linear progression) for our rank ladder. The problem is that your smart superusers will most likely figure out this ranking scheme.
So, how do you keep the superusers engaged under such predictable (boring) ranking criteria? I will describe 4 strategies that you can do to spice up your rank ladder even when it is a predictable and boring arithmetic progression.
5.1 Name Your Ranks Creatively
It is inevitable that some superusers will eventually figure out the post requirement for promotion, and will expect a promotion at the right time. But if you name your ranks cleverly, they still won’t know what they are going to get next. So, don’t name your ranks in any obvious progression. For example, a terrible choice of rank names would be bronze, silver, etc. Without even writing it down, it is blatantly obvious that the one after silver is going to be gold, then probably platinum, titanium, and then diamond. Give your superusers some serendipitous joy when they get promoted and use your imagination when naming your ranks.
5.2 Make Some Noise
For statisticians, there is a simple trick to make things less predictable. Just add some
For example, it is very easy for anyone to figure out the pattern in the following linear progression: 10, 20, 30, 40, 50, 60, 70, etc. By adding some random noise, the sequence becomes much harder to predict: 11, 18, 32, 41, 49, 63, 74, etc.
Notice that the challenges between the ranks will remain roughly the same (compare the jagged ranking criteria here in
5.3 Privileges Do Matter
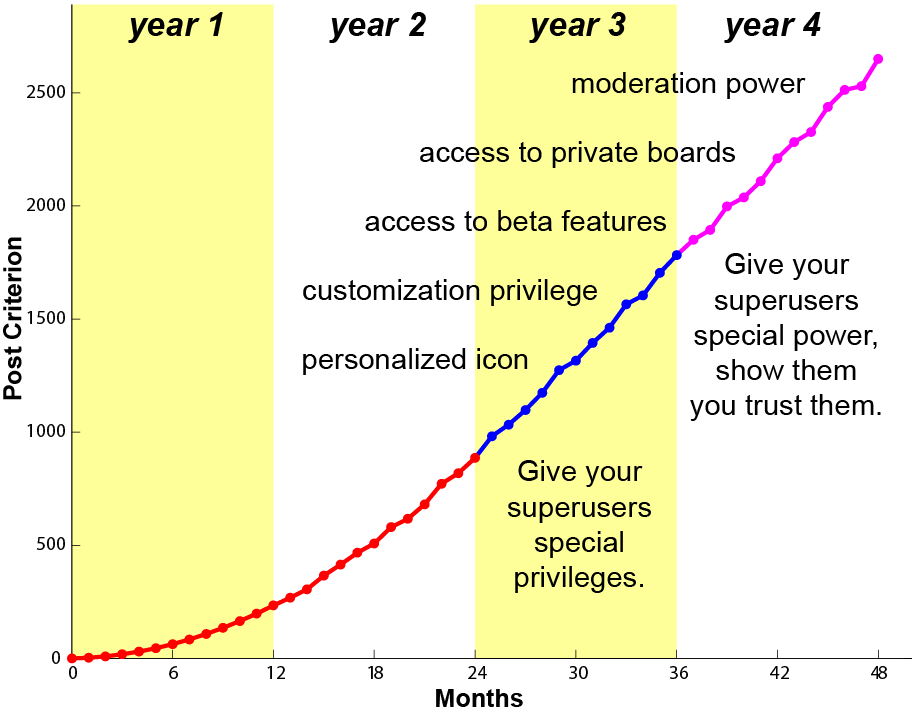
Even with added noise and the most humorous and interesting rank names, superusers may still get tired of the routine rank changes without other incentives. This is especially true after you switch the ranking criteria over to the highly predictable linear progressions to avoid over-challenging your superusers. If you follow the recommendation in this whitepaper, this should happen roughly 2 years after the superuser first participated in the community.
After 2 years, don’t you think it is time to show your superusers that you recognize how special they are? So tell them (it only takes an email) and grant them access and customization privileges that are not available to others. Start with something simple, such as allowing your superusers to use a personalized icon. Then as they move up the rank ladder, they will be intermittently rewarded with different privileges that are totally unpredictable.
Attaching special privileges to a rank through the permission system is an extremely effective way to engage your superusers. However, you might want to let time test their loyalty and goodwill before giving out too many privileges. Therefore the perfect time to give out special privileges is after the superusers have moved through the first 24 ranks. However, if you really trust your superusers, you may do this earlier on your rank ladder. This also applies when recruiting your superusers into MVP programs.
5.4 Show Your Trust
An important reason to give special permissions to your superusers is to establish trust. A deep relationship built on trust is likely to be more lasting than a superficial relationship that is built on incentives. So show your superusers that you trust them. Invite them to beta-test programs in private boards and treat them as your most valuable assets. Give them the power to take action in the community, such as moving posts and perhaps deleting inappropriate content. Let them help you moderate your community.
Can you really trust the superusers with that much power? I believe that you can and you should. Because it is highly improbable that a superuser would just throw away all the reputations and privileges they’ve earned through hard work over a long period of time. The more they have invested, the more they will treasure their unique social status.
Now that your rank ladder is all spiced up, you should be able to keep your superusers engaged indefinitely (contrast Figure 5.1 above with Figure 4.1).
6. Building a Complete Rank Structure
We’ve covered a lot of ground, and I’ve introduced many design principles for building an optimal rank ladder for engaging your superusers. I must emphasize that it is very important to implement these rank design principles in the order that they are presented. It is meaningless to flow with your superusers, if you don’t know your superusers’ capability. And it is useless trying to surprise your superusers with special privileges if the gaps between your ranks are so large that it takes them years to get a promotion. They will never get there and never be surprised! However, the first two steps do involve some analytical work, and they are the most difficult and most important steps (especially the steps in Section 3). Once you know your superusers, everything that follows is easy.
Until now, I have been talking about the principles for designing a single rank ladder that rewards the posting behavior of community members. Although message posting is a common mode of participation within online communities, modern community platforms now furnish their members with a host of activities. Consequently, superusers may come in many flavors depending on the kinds of activity they participate in.
The superusers that we’ve considered so far are content creators who excel in posting messages. But superusers may be critics who rate content by giving kudos and reporting inappropriate content, and others may be organizers who label and tag content. Therefore, an ideal rank structure should have multiple branches for rewarding different kinds of participation (Figure 6.1).
To create a multi-branch rank structure, you simply juxtapose several rank ladders together. Each ladder has a set of ranking criteria that is based on different participation metrics. For example, rather than post requirement, some ladders may use kudos requirements, and others may have a tag count requirement. Based on the superusers’ participation, they will climb different ladders. Some well-rounded superusers may even excel on several ladders. Moreover, rank ladders can be merged by creating participation criteria using the logical conjunction
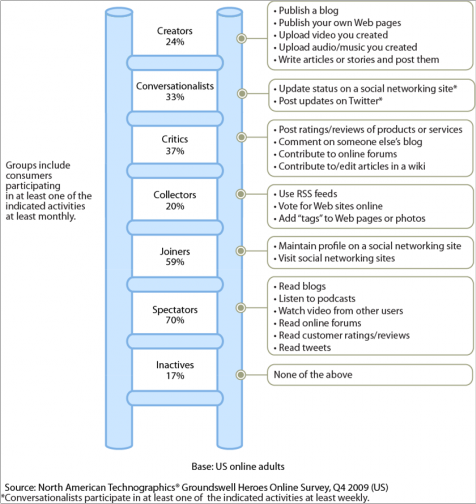
So how many branches should you have? According to Forrester Research, online participation patterns can be segmented into 7 categories via the social technographic profile. And they include inactives, spectators, joiners, collectors, critics, conversationalists, and creators (Figure 6.2). Since the inactives do not participate, and spectators only consume content passively, there are at least 5 categories of active participation that you can reward. But in theory, there is no limit to how many branches you could have in your rank structure.
The more ladders you have, the more unique your superusers will feel about their contribution (and reward). But more ladders required more management. A multi-branch rank structure should be the last step in the design of your rank structure. Having many poorly designed rank ladders is much worse than having one that is well-designed.
My advice is to start with one ladder for your creators using only the post-count metric. When you are able to manage the steps described from Section 2 to Section 5 with all the yearly adjustments, then you can add another ladder for your conversationalists, and then the critics, then the collectors, and finally the joiners.
7. Conclusion
In conclusion, this whitepaper presents a strategic blueprint for designing an effective rank structure that engages and motivates active participation in any online community. By understanding the principles of creating a “flow” state, we can align rank criteria with users’ capabilities. Moreover, by injecting unpredictability (surprises), and adapting over time, community managers can foster vibrant and dynamic communities.
It is important to emphasize that the application of these principles goes beyond just online communities. They can be readily applied to various use cases of gamification, such as employee engagement programs, customer loyalty initiatives, and educational platforms. The concept of “flow” and thoughtful rank (or level) design can elevate participation and drive meaningful interactions in any context.
In a rapidly changing digital landscape, the strategies outlined in this whitepaper offer a roadmap to create engaging and rewarding experiences for any audience. Beyond the highly popular gamification use cases above, they can cultivate user loyalty, and achieve long-term success across many different domains. Within an enterprise, these include enterprise collaboration, product innovation, technology adoption, employee well-being, enterprise knowledge retention, changing public perceptions, driving workforce passion, and even changing corporate culture. Beyond enterprise, there may be societal and individual applications too. For example, healthy habit formation (dieting, exercising, etc.), retirement planning, continuing education, responsible borrowing, and even civic engagement.
If you are reading this, congratulation! This concludes the discussion on designing the optimal rank structure. Now you know the key ingredients to build a lively and vibrant community (online or offline), in companies, societies, or nations. Now, it is up to you to make our world a better place.